Post by Shipfish on Jan 19, 2012 21:31:54 GMT -6
So.
Time travel.
It's easier than it looks.
So I drew up a lovely guide to all of you, but apparently it isn't easy to decipher. Thus, this thread!
What is time travel?
Time travel is travel forward or back on a time continuum (that is, a straight line). This works because in normal space, you can move up/down, left/right, forward/back; while in time you can only move forward/back. 3D versus 1D, really it's elementary stuff.
Unfortunately, one dimensional time has a bigger effect on our life than a dimension of space does. Because of time, organisms can grow, dead things can rot, generally Stuff Happens. And (as we know) once Something Happens, we cannot undo it. But what if we could?
This brings up the notion of a paradox. The paradox most likely to come up is the predestination paradox: the most famous example is Oedipus. It can also be thought of as a self-fulfilling prophecy, only with time travel. Example: Harry Potter is saved by a stag patronus by a lake. He believes it is his father, until he finds himself right next to that lake in exactly the same position. Time itself "set him up" to close the loop. The second most common is the grandfather paradox: you are probably familiar with this one. The idea is that you use time travel to make it impossible for you to time travel in the first place, which makes it impossible to prevent yourself from time travelling, which makes it so you go back and prevent yourself from travelling ad nauseam. The last is the bootstrap paradox, which may need a bit of explaining. In this paradox, an item or a piece of information is trapped in a closed timelike curve. After the information or the object is sent back in time, it is recovered in the present and becomes the very object/information that was initially sent back in time in the first place. Unfortunately, this only really works for information, since any object caught in a loop like this would immediately age to infinity, causing it to become dust (and thus not enter the loop in the first place, see grandfather paradox).
If you stuck with me through that, congrats. I'm pretty sure it gets easier from here.
How do you propose to keep track of all this nonsense?
What a lovely question! I have just the answer!
It's graphs! The answer is graphs!
Ok, so maybe that wasn't really clear.
Think of a car going from one place to another. Travelling to and from these places takes time, right? Let's make it so that the car can stay at any location it wants for as long as it wants, and takes one Time Unit to move between places. Alright.
Let's graph the location of the car against the total amount of time it has been driving around willy-nilly.
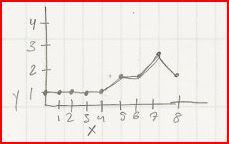
X= time; Y= location
You can see that the car has been around for eight hours, and has visited three locations. It stayed at Location One for four hours, moved to Location Two, stayed for an hour, moved to Location Three and then immediately left for Location Two again (apparently Three isn't so hot).
Not complicated at all, you've been doing these kind of things in science class since you were really little, plotting temperature against time, plotting score against time, pretty much everything. Not hard at all.
So this is where people get confused. In the above example with the car, the car was capable only of moving through time in one direction: forward. (Remember, time is on X and location is on Y.) If the car can move through time in any direction it wants, then it can be much less confusing if you add another axis, this time Z. Z will track our car based on it's own personal time. Note: It is still possible to graph a time traveller's movements on just a plain (X,Y) coordinate plane, but it is much easier to understand if you add Z to make a coordinate cube.
So: let's rename our axes. X used to be plain old time, but we are going to set it to Objective Time now. What I mean by objective time is time as experience by everyone: we travel to the future at precisely one second per second. If you set a clock on the ground and didn't mess with it, it would be recording objective time. (etime [everyonetime] for short!)
Y is still going to be location. Good ol' Y, you lived through time travel.
Z, our new axis, is going to be named Subjective Time. By subjective, I mean if you strapped a clock to a time traveller, set it to twelve, sent him back to the Cretaceous and made him wait an hour before coming back, the clock would read one in the afternoon. It is time as experienced by the traveller. (ktime [Kyanastime] for short!)
Yay! Still with me? Good. I'm going to start showing you pictures now, don't get frightened.

Remember, X= everyonetime; Y= location; Z= Kyanastime
I gave you the ktime/location graph first because it is easy to see the progression: the time traveller goes from Location One to Location Two to Location Three. Simple, easy, effective.
Here, to make it even more nice, I'm going to show you the table I made with these three graphs. The table shows X, Y, and Z values with an event column to help make sense of things. Notice how the Z column goes from 0 to 9 without moving around: this is because time will move linearly for the time traveller.
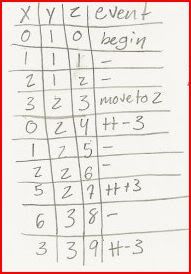
tt stands for time travel: tt+3 would be jumping ahead three hours.
That wasn't bad. Now, look back at the table and notice how the X value (etime) is jumping around. This is because the traveller is moving about in time. Here is the graph of etime/location. The red is how it would look if I drew all the lines straight, and the curved lines in pencil are there to show you how they actually connect up.
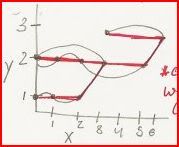
Hideously complex, I know. Notice how it is possible to be in multiple places at one slice of time: at X=2, there are two Y values. (Thus a personal joke I made up: Time travellers are not functions! You know it was funny.)
One last graph and I will let you go. This one is the most conceptually confusing. It plots Z against X. I know you are thinking "Did I hear that wrong? Are we going to graph two time-axes against each other?" You heard me correctly. We are going to graph etime/ktime. Notice that I put Z at the bottom, even though it is technically more correct to put X there. I just think it looks better.
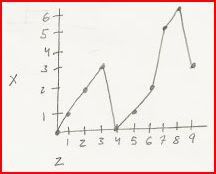
Indeed.
Oddly enough, you may notice a pattern. On a normal person's graph, X will always equal Z. This is because their subjective time is exactly the same as the objective time. On a time traveller's graph however, the line can and does deviate from X=Z. One can even say that the time traveller is "before" or "after" a point in etime by drawing a line through X=Z and marking anything above it as "after" and below as "before."
Oh dear lord. I didn't get any of that.
Oh, it's fine, I guess. I did try. If you have any questions, please post them in the cbox or on this thread. Probably on this thread, since you might clutter up the box.
Note: this was never intended to be explained to anyone other than me. I made it up for fun.
Time travel.
It's easier than it looks.
So I drew up a lovely guide to all of you, but apparently it isn't easy to decipher. Thus, this thread!
What is time travel?
Time travel is travel forward or back on a time continuum (that is, a straight line). This works because in normal space, you can move up/down, left/right, forward/back; while in time you can only move forward/back. 3D versus 1D, really it's elementary stuff.
Unfortunately, one dimensional time has a bigger effect on our life than a dimension of space does. Because of time, organisms can grow, dead things can rot, generally Stuff Happens. And (as we know) once Something Happens, we cannot undo it. But what if we could?
This brings up the notion of a paradox. The paradox most likely to come up is the predestination paradox: the most famous example is Oedipus. It can also be thought of as a self-fulfilling prophecy, only with time travel. Example: Harry Potter is saved by a stag patronus by a lake. He believes it is his father, until he finds himself right next to that lake in exactly the same position. Time itself "set him up" to close the loop. The second most common is the grandfather paradox: you are probably familiar with this one. The idea is that you use time travel to make it impossible for you to time travel in the first place, which makes it impossible to prevent yourself from time travelling, which makes it so you go back and prevent yourself from travelling ad nauseam. The last is the bootstrap paradox, which may need a bit of explaining. In this paradox, an item or a piece of information is trapped in a closed timelike curve. After the information or the object is sent back in time, it is recovered in the present and becomes the very object/information that was initially sent back in time in the first place. Unfortunately, this only really works for information, since any object caught in a loop like this would immediately age to infinity, causing it to become dust (and thus not enter the loop in the first place, see grandfather paradox).
If you stuck with me through that, congrats. I'm pretty sure it gets easier from here.
How do you propose to keep track of all this nonsense?
What a lovely question! I have just the answer!
It's graphs! The answer is graphs!
Ok, so maybe that wasn't really clear.
Think of a car going from one place to another. Travelling to and from these places takes time, right? Let's make it so that the car can stay at any location it wants for as long as it wants, and takes one Time Unit to move between places. Alright.
Let's graph the location of the car against the total amount of time it has been driving around willy-nilly.

X= time; Y= location
You can see that the car has been around for eight hours, and has visited three locations. It stayed at Location One for four hours, moved to Location Two, stayed for an hour, moved to Location Three and then immediately left for Location Two again (apparently Three isn't so hot).
Not complicated at all, you've been doing these kind of things in science class since you were really little, plotting temperature against time, plotting score against time, pretty much everything. Not hard at all.
So this is where people get confused. In the above example with the car, the car was capable only of moving through time in one direction: forward. (Remember, time is on X and location is on Y.) If the car can move through time in any direction it wants, then it can be much less confusing if you add another axis, this time Z. Z will track our car based on it's own personal time. Note: It is still possible to graph a time traveller's movements on just a plain (X,Y) coordinate plane, but it is much easier to understand if you add Z to make a coordinate cube.
So: let's rename our axes. X used to be plain old time, but we are going to set it to Objective Time now. What I mean by objective time is time as experience by everyone: we travel to the future at precisely one second per second. If you set a clock on the ground and didn't mess with it, it would be recording objective time. (etime [everyonetime] for short!)
Y is still going to be location. Good ol' Y, you lived through time travel.
Z, our new axis, is going to be named Subjective Time. By subjective, I mean if you strapped a clock to a time traveller, set it to twelve, sent him back to the Cretaceous and made him wait an hour before coming back, the clock would read one in the afternoon. It is time as experienced by the traveller. (ktime [Kyanastime] for short!)
Yay! Still with me? Good. I'm going to start showing you pictures now, don't get frightened.

Remember, X= everyonetime; Y= location; Z= Kyanastime
I gave you the ktime/location graph first because it is easy to see the progression: the time traveller goes from Location One to Location Two to Location Three. Simple, easy, effective.
Here, to make it even more nice, I'm going to show you the table I made with these three graphs. The table shows X, Y, and Z values with an event column to help make sense of things. Notice how the Z column goes from 0 to 9 without moving around: this is because time will move linearly for the time traveller.

tt stands for time travel: tt+3 would be jumping ahead three hours.
That wasn't bad. Now, look back at the table and notice how the X value (etime) is jumping around. This is because the traveller is moving about in time. Here is the graph of etime/location. The red is how it would look if I drew all the lines straight, and the curved lines in pencil are there to show you how they actually connect up.

Hideously complex, I know. Notice how it is possible to be in multiple places at one slice of time: at X=2, there are two Y values. (Thus a personal joke I made up: Time travellers are not functions! You know it was funny.)
One last graph and I will let you go. This one is the most conceptually confusing. It plots Z against X. I know you are thinking "Did I hear that wrong? Are we going to graph two time-axes against each other?" You heard me correctly. We are going to graph etime/ktime. Notice that I put Z at the bottom, even though it is technically more correct to put X there. I just think it looks better.

Indeed.
Oddly enough, you may notice a pattern. On a normal person's graph, X will always equal Z. This is because their subjective time is exactly the same as the objective time. On a time traveller's graph however, the line can and does deviate from X=Z. One can even say that the time traveller is "before" or "after" a point in etime by drawing a line through X=Z and marking anything above it as "after" and below as "before."
Oh dear lord. I didn't get any of that.
Oh, it's fine, I guess. I did try. If you have any questions, please post them in the cbox or on this thread. Probably on this thread, since you might clutter up the box.
Note: this was never intended to be explained to anyone other than me. I made it up for fun.

